Relaxed
(fps/relaxed.hpp)

• View this file on GitHub
• Last update: 2025-10-26 03:52:03+09:00
• Include: #include "fps/relaxed.hpp"

多項式 $f(x),g(x)$ について $i=0,1,\dots$ について順に以下を処理する．

$[x^i]f(x),[x^i]g(x)$ が新しく与えられる．$[x^i]f(x)g(x)$ を返す．

$N$ 次まで求めるとき $O(N(\log N)^2)$ 時間．

$g$ がはじめからわかっている場合 (semi-relaxed convolution) は定数倍が改善できる．

また inv/exp/log/sqrt なども積と同じ計算量で求められる．

積

適切に分割してまとめて計算する．

通常の畳み込みよりも middle product の方が相性がよい．

• https://qiita.com/Kiri8128/items/1738d5403764a0e26b4c

上の資料で middle product の項で提示されている形よりは以下の形の方が扱いやすいはず

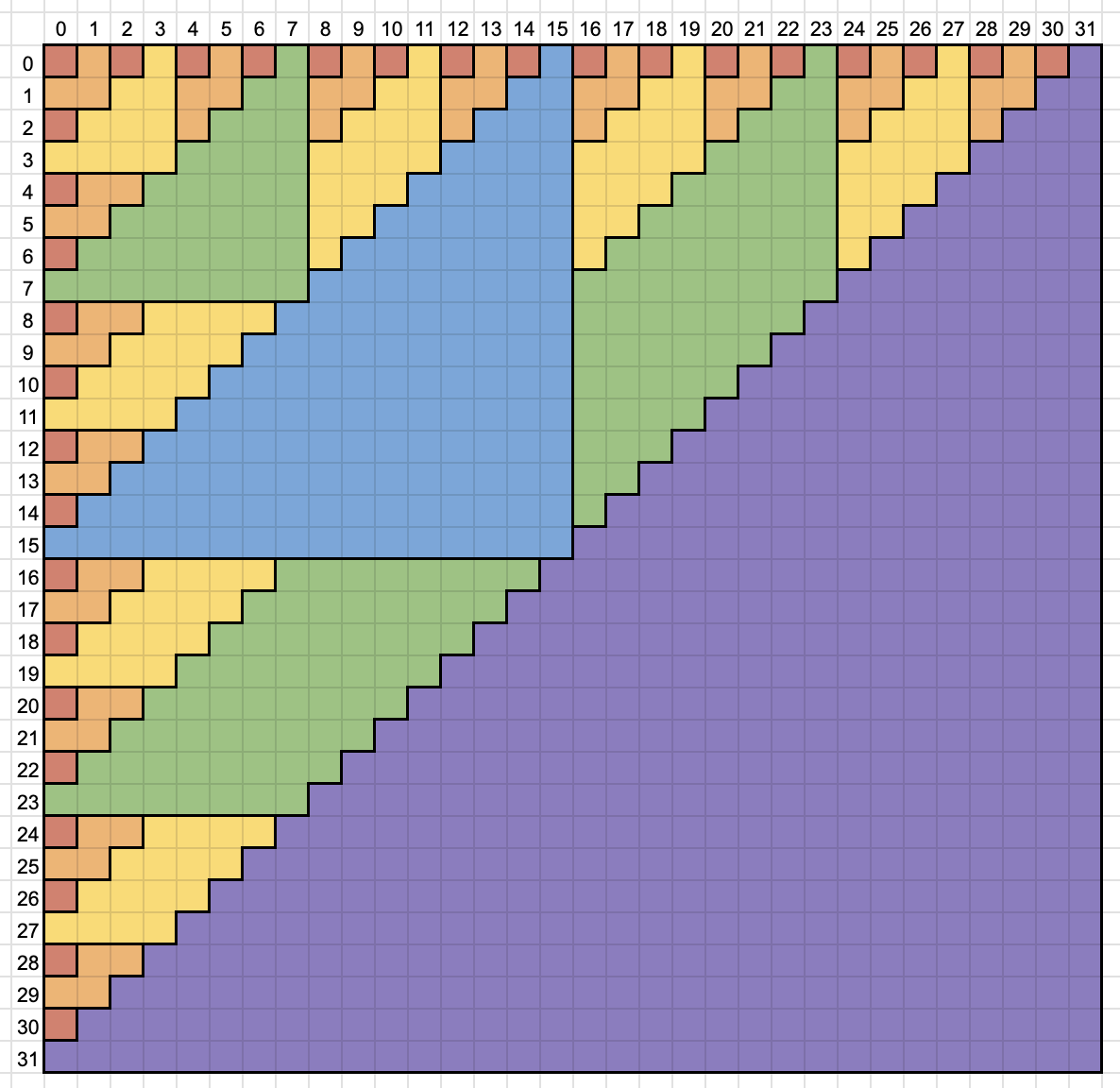
inv / FPS 除算

より一般に $h(x)=f(x)/g(x)$ を求めることができる（$[x^0]g(x)\neq 0$）．

$f=gh$ より任意の $i$ に対し

\[h_i=\frac{1}{g_0}\left(f_i-\sum_{j=0}^{i-1}h_{i-1-j}g_{j+1}\right)\]

であるから積の計算に帰着される（特に定数倍は変化しない）．

exp

$g(x)=\exp f(x)\ ([x^0]f(x)=0)$ のとき $g_0=1$ である．また $g’=f’g$ より $1$ 次以上の部分は積の計算に帰着される．

log

$g(x)=\log f(x)\ ([x^0]f(x)=1)$ のとき $g_0=0$ である．また $g’=f’/f$ より $1$ 次以上の部分は FPS の除算に帰着される．

sqrt

$g(x)=\sqrt{f(x)}\ ([x^0]f(x)\neq 0)$ のとき $g_0=\sqrt{f_0}$ である．また $g^2=f$ より $i\geq 1$ について

\[2g_0g_i+\sum_{j=1}^{i-1}g_jg_{i-j}=f_i\]

であるから積の計算に帰着できる．

Depends on

• fps/formal-power-series.hpp
• 階乗, 二項係数 (modint/factorial.hpp)
• modint/mod-pow.hpp
• modint/mod-sqrt.hpp

Verified with

• verify/fps/LC_convolution_mod.relaxed.test.cpp
• verify/fps/LC_convolution_mod.semirelaxed.test.cpp
• verify/fps/LC_exp_of_formal_power_series.relaxed.test.cpp
• verify/fps/LC_inv_of_formal_power_series.relaxed.test.cpp
• verify/fps/LC_log_of_formal_power_series.relaxed.test.cpp
• verify/fps/LC_sqrt_of_formal_power_series.relaxed.test.cpp

Code

#pragma once
#include "modint/factorial.hpp"
#include "fps/formal-power-series.hpp"
#include "modint/mod-sqrt.hpp"

template <class mint>
class RelaxedMultiply {
  const int B = 6;
  using fps = FormalPowerSeries<mint>;
  int n;
  fps f, g, h;
  vector<fps> f0, g0;

 public:
  RelaxedMultiply() : n(0), f(1), g(1), f0(B), g0(B) {}
  mint append(mint a, mint b) {
    f[n] = a, g[n] = b;
    n++;
    int m = n & -n;
    int l = __builtin_ctz((unsigned int)m);
    if (n == m) {
      f.resize(2 * m);
      g.resize(2 * m);
      h.resize(2 * m);
      if (l < B) {
        for (int i = 0; i < m; i++)
          for (int j = m - 1 - i; j < m; j++)
            h[i + j] += f[i] * g[j];
      } else {
        auto f1 = f;
        f1.ntt();
        f0.push_back(fps(f1.begin(), f1.begin() + m));
        auto g1 = g;
        g1.ntt();
        g0.push_back(fps(g1.begin(), g1.begin() + m));
        for (int i = 0; i < 2 * m; i++) f1[i] *= g1[i];
        f1.intt();
        for (int i = m - 1; i < 2 * m - 1; i++) h[i] += f1[i];
      }
    } else {
      if (l < B) {
        int s = n - m;
        for (int i = 0; i < m; i++) {
          int t = m - 1 - i;
          for (int j = 0; j < m; j++)
            h[n - 1 + j] += f[s + i] * g[t + j] + g[s + i] * f[t + j];
        }
      } else {
        fps f1(2 * m), g1(2 * m), h1(2 * m);
        copy(f.begin() + (n - m), f.begin() + n, f1.begin());
        copy(g.begin() + (n - m), g.begin() + n, g1.begin());
        f1.ntt(), g1.ntt();
        for (int i = 0; i < 2 * m; i++) h1[i] += f1[i] * g0[l + 1][i] + f0[l + 1][i] * g1[i];
        h1.intt();
        for (int i = m - 1; i < 2 * m - 1; i++) h[n - m + i] += h1[i];
      }
    }
    return h[n - 1];
  }
};

template <class mint>
class SemiRelaxedMultiply {
  const int B = 6;
  using fps = FormalPowerSeries<mint>;
  int n, m0;
  fps f, g, h;
  vector<fps> g0;

 public:
  SemiRelaxedMultiply(const fps& g_) : n(0), m0(1 << B), f(1), g(g_) {
    while (m0 < g.size()) m0 <<= 1;
    g.resize(m0);
    for (int k = 1; k <= m0; k <<= 1) {
      fps g1(2 * k);
      copy(g.begin(), g.begin() + min(2 * k, m0), g1.begin());
      g1.ntt();
      g0.push_back(g1);
    }
  }
  mint append(mint a) {
    f[n] = a;
    n++;
    int m = n & -n;
    int l = __builtin_ctz((unsigned int)m);
    if (n == m) {
      f.resize(2 * m);
      h.resize(2 * m);
    }
    while (l >= g0.size()) {
      g0.push_back(g0.back());
      g0.back().ntt_doubling();
    }
    if (l < B) {
      int s = n - m;
      for (int i = 0; i < m; i++) {
        int t = m - 1 - i;
        for (int j = 0; j < m; j++)
          h[n - 1 + j] += f[s + i] * g[t + j];
      }
    } else {
      fps f1(2 * m);
      copy(f.begin() + (n - m), f.begin() + n, f1.begin());
      f1.ntt();
      for (int i = 0; i < 2 * m; i++) f1[i] *= g0[l][i];
      f1.intt();
      for (int i = m - 1; i < 2 * m - 1; i++) h[n - m + i] += f1[i];
    }
    return h[n - 1];
  }
};

// f(x)/g(x)
template <class mint>
class RelaxedDivide {
  RelaxedMultiply<mint> mul;
  int n;
  mint c, v;

 public:
  RelaxedDivide() : n(0) {}
  mint append(mint a, mint b) { return v = n++ == 0 ? a * (c = b.inv()) : (a - mul.append(v, b)) * c; }
};

template <class mint>
class RelaxedInv {
  RelaxedMultiply<mint> mul;
  int n;
  mint c, v;

 public:
  RelaxedInv() : n(0) {}
  mint append(mint a) { return v = n++ == 0 ? (c = a.inv()) : -mul.append(v, a) * c; }
};

template <class mint>
class RelaxedExp {
  using fact = Factorial<mint>;
  RelaxedMultiply<mint> mul;
  int n;
  mint v;

 public:
  RelaxedExp() : n(0) {}
  mint append(mint a) {
    if (n++ == 0) {
      assert(a == 0);
      v = 1;
    } else {
      v = mul.append((n - 1) * a, v) * fact::inv(n - 1);
    }
    return v;
  }
};

template <class mint>
class RelaxedLog {
  using fact = Factorial<mint>;
  RelaxedMultiply<mint> mul;
  int n;
  mint a0, v;

 public:
  RelaxedLog() : n(0) {}
  mint append(mint a) {
    if (n == 0) {
      assert(a == 1);
      n++;
      return 0;
    } else if (n == 1) {
      a0 = a, n++;
      return v = a;
    } else {
      v = n * a - mul.append(v, a0);
      a0 = a;
      return v * fact::inv(n++);
    }
  }
};

template <class mint>
class RelaxedSqrt {
  RelaxedMultiply<mint> mul;
  int n;
  mint c, v;

 public:
  RelaxedSqrt() : n(0) {}
  mint append(mint a) {
    if (n == 0) {
      long long sq = ModSqrt(a.val(), mint::get_mod());
      assert(sq != -1 && sq != 0);
      c = mint(2 * sq).inv();
      n++;
      return sq;
    } else {
      return v = (n++ == 1 ? a : a - mul.append(v, v)) * c;
    }
  }
};

/**
 * @brief Relaxed 
 * @docs docs/fps/relaxed.md
 */

#line 2 "modint/factorial.hpp"

template <class mint>
struct Factorial {
  static void reserve(int n) {
    inv(n);
    fact(n);
    fact_inv(n);
  }
  static mint inv(int n) {
    static long long mod = mint::get_mod();
    static vector<mint> buf({0, 1});
    assert(n != 0);
    if (mod != mint::get_mod()) {
      mod = mint::get_mod();
      buf = vector<mint>({0, 1});
    }
    while ((int)buf.capacity() <= n) buf.reserve(buf.capacity() * 2);
    while ((int)buf.size() <= n) {
      long long k = buf.size(), q = (mod + k - 1) / k;
      buf.push_back(q * buf[k * q - mod]);
    }
    return buf[n];
  }
  static mint fact(int n) {
    static long long mod = mint::get_mod();
    static vector<mint> buf({1, 1});
    assert(n >= 0);
    if (mod != mint::get_mod()) {
      mod = mint::get_mod();
      buf = vector<mint>({1, 1});
    }
    while ((int)buf.capacity() <= n) buf.reserve(buf.capacity() * 2);
    while ((int)buf.size() <= n) {
      long long k = buf.size();
      buf.push_back(buf.back() * k);
    }
    return buf[n];
  }
  static mint fact_inv(int n) {
    static long long mod = mint::get_mod();
    static vector<mint> buf({1, 1});
    assert(n >= 0);
    if (mod != mint::get_mod()) {
      mod = mint::get_mod();
      buf = vector<mint>({1, 1});
    }
    if ((int)buf.size() <= n) inv(n);
    while ((int)buf.capacity() <= n) buf.reserve(buf.capacity() * 2);
    while ((int)buf.size() <= n) {
      long long k = buf.size();
      buf.push_back(buf.back() * inv(k));
    }
    return buf[n];
  }
  static mint binom(int n, int r) {
    if (r < 0 || r > n) return 0;
    return fact(n) * fact_inv(r) * fact_inv(n - r);
  }
  static mint binom_naive(int n, int r) {
    if (r < 0 || r > n) return 0;
    mint res = fact_inv(r);
    for (int i = 0; i < r; i++) res *= n - i;
    return res;
  }
  static mint multinom(const vector<int>& r) {
    int n = 0;
    for (auto& x : r) {
      if (x < 0) return 0;
      n += x;
    }
    mint res = fact(n);
    for (auto& x : r) res *= fact_inv(x);
    return res;
  }
  static mint P(int n, int r) {
    if (r < 0 || r > n) return 0;
    return fact(n) * fact_inv(n - r);
  }
  // partition n items to r groups (allow empty group)
  static mint H(int n, int r) {
    if (n < 0 || r < 0) return 0;
    return r == 0 ? 1 : binom(n + r - 1, r);
  }
};
/**
 * @brief 階乗, 二項係数
 */
#line 2 "fps/formal-power-series.hpp"

template <class mint>
struct FormalPowerSeries : vector<mint> {
  using vector<mint>::vector;
  using FPS = FormalPowerSeries;
  FPS &operator+=(const FPS &r) {
    if (r.size() > this->size()) this->resize(r.size());
    for (int i = 0; i < (int)r.size(); i++) (*this)[i] += r[i];
    return *this;
  }
  FPS &operator+=(const mint &r) {
    if (this->empty()) this->resize(1);
    (*this)[0] += r;
    return *this;
  }
  FPS &operator-=(const FPS &r) {
    if (r.size() > this->size()) this->resize(r.size());
    for (int i = 0; i < (int)r.size(); i++) (*this)[i] -= r[i];
    return *this;
  }
  FPS &operator-=(const mint &r) {
    if (this->empty()) this->resize(1);
    (*this)[0] -= r;
    return *this;
  }
  FPS &operator*=(const mint &v) {
    for (int k = 0; k < (int)this->size(); k++) (*this)[k] *= v;
    return *this;
  }
  FPS &operator/=(const FPS &r) {
    if (this->size() < r.size()) {
      this->clear();
      return *this;
    }
    int n = this->size() - r.size() + 1;
    if ((int)r.size() <= 64) {
      FPS f(*this), g(r);
      g.shrink();
      mint coeff = g.at(g.size() - 1).inv();
      for (auto &x : g) x *= coeff;
      int deg = (int)f.size() - (int)g.size() + 1;
      int gs = g.size();
      FPS quo(deg);
      for (int i = deg - 1; i >= 0; i--) {
        quo[i] = f[i + gs - 1];
        for (int j = 0; j < gs; j++) f[i + j] -= quo[i] * g[j];
      }
      *this = quo * coeff;
      this->resize(n, mint(0));
      return *this;
    }
    return *this = ((*this).rev().pre(n) * r.rev().inv(n)).pre(n).rev();
  }
  FPS &operator%=(const FPS &r) {
    *this -= *this / r * r;
    shrink();
    return *this;
  }
  FPS operator+(const FPS &r) const { return FPS(*this) += r; }
  FPS operator+(const mint &v) const { return FPS(*this) += v; }
  FPS operator-(const FPS &r) const { return FPS(*this) -= r; }
  FPS operator-(const mint &v) const { return FPS(*this) -= v; }
  FPS operator*(const FPS &r) const { return FPS(*this) *= r; }
  FPS operator*(const mint &v) const { return FPS(*this) *= v; }
  FPS operator/(const FPS &r) const { return FPS(*this) /= r; }
  FPS operator%(const FPS &r) const { return FPS(*this) %= r; }
  FPS operator-() const {
    FPS ret(this->size());
    for (int i = 0; i < (int)this->size(); i++) ret[i] = -(*this)[i];
    return ret;
  }
  void shrink() {
    while (this->size() && this->back() == mint(0)) this->pop_back();
  }
  FPS rev() const {
    FPS ret(*this);
    reverse(begin(ret), end(ret));
    return ret;
  }
  FPS dot(FPS r) const {
    FPS ret(min(this->size(), r.size()));
    for (int i = 0; i < (int)ret.size(); i++) ret[i] = (*this)[i] * r[i];
    return ret;
  }
  FPS pre(int sz) const {
    return FPS(begin(*this), begin(*this) + min((int)this->size(), sz));
  }
  FPS operator>>=(int sz) {
    assert(sz >= 0);
    if ((int)this->size() <= sz) return {};
    this->erase(this->begin(), this->begin() + sz);
    return *this;
  }
  FPS operator>>(int sz) const {
    if ((int)this->size() <= sz) return {};
    FPS ret(*this);
    ret.erase(ret.begin(), ret.begin() + sz);
    return ret;
  }
  FPS operator<<=(int sz) {
    assert(sz >= 0);
    this->insert(this->begin(), sz, mint(0));
    return *this;
  }
  FPS operator<<(int sz) const {
    FPS ret(*this);
    ret.insert(ret.begin(), sz, mint(0));
    return ret;
  }
  FPS diff() const {
    const int n = (int)this->size();
    FPS ret(max(0, n - 1));
    mint one(1), coeff(1);
    for (int i = 1; i < n; i++) {
      ret[i - 1] = (*this)[i] * coeff;
      coeff += one;
    }
    return ret;
  }
  FPS integral() const {
    const int n = (int)this->size();
    FPS ret(n + 1);
    ret[0] = mint(0);
    if (n > 0) ret[1] = mint(1);
    auto mod = mint::get_mod();
    for (int i = 2; i <= n; i++) ret[i] = (-ret[mod % i]) * (mod / i);
    for (int i = 0; i < n; i++) ret[i + 1] *= (*this)[i];
    return ret;
  }
  mint eval(mint x) const {
    mint r = 0, w = 1;
    for (auto &v : *this) r += w * v, w *= x;
    return r;
  }
  FPS log(int deg = -1) const {
    assert((*this)[0] == mint(1));
    if (deg == -1) deg = (int)this->size();
    return (this->diff() * this->inv(deg)).pre(deg - 1).integral();
  }
  FPS pow(int64_t k, int deg = -1) const {
    const int n = (int)this->size();
    if (deg == -1) deg = n;
    if (k == 0) {
      FPS ret(deg);
      if (deg) ret[0] = 1;
      return ret;
    }
    for (int i = 0; i < n; i++) {
      if ((*this)[i] != mint(0)) {
        mint rev = mint(1) / (*this)[i];
        FPS ret = (((*this * rev) >> i).log(deg) * k).exp(deg);
        ret *= (*this)[i].pow(k);
        ret = (ret << (i * k)).pre(deg);
        if ((int)ret.size() < deg) ret.resize(deg, mint(0));
        return ret;
      }
      if (__int128_t(i + 1) * k >= deg) return FPS(deg, mint(0));
    }
    return FPS(deg, mint(0));
  }

  static void *ntt_ptr;
  static void set_ntt();
  FPS &operator*=(const FPS &r);
  FPS middle_product(const FPS &r) const;
  void ntt();
  void intt();
  void ntt_doubling();
  static int ntt_root();
  FPS inv(int deg = -1) const;
  FPS exp(int deg = -1) const;
};
template <typename mint>
void *FormalPowerSeries<mint>::ntt_ptr = nullptr;
#line 2 "modint/mod-sqrt.hpp"

#line 2 "modint/mod-pow.hpp"

unsigned int ModPow(unsigned int a, unsigned long long n, unsigned int m) {
  unsigned long long x = a, y = 1;
  while (n) {
    if (n & 1) y = y * x % m;
    x = x * x % m;
    n >>= 1;
  }
  return y;
}
#line 4 "modint/mod-sqrt.hpp"

long long ModSqrt(long long a, long long p) {
  if (a >= p) a %= p;
  if (p == 2) return a & 1;
  if (a == 0) return 0;
  if (ModPow(a, (p - 1) / 2, p) != 1) return -1;
  if (p % 4 == 3) return ModPow(a, (3 * p - 1) / 4, p);
  unsigned int z = 2, q = p - 1;
  while (ModPow(z, (p - 1) / 2, p) == 1) z++;
  int s = 0;
  while (!(q & 1)) {
    s++;
    q >>= 1;
  }
  int m = s;
  unsigned int c = ModPow(z, q, p);
  unsigned int t = ModPow(a, q, p);
  unsigned int r = ModPow(a, (q + 1) / 2, p);
  while (true) {
    if (t == 1) return r;
    unsigned int pow = t;
    int j = 1;
    for (; j < m; j++) {
      pow = 1ll * pow * pow % p;
      if (pow == 1) break;
    }
    unsigned int b = c;
    for (int i = 0; i < m - j - 1; i++) b = 1ll * b * b % p;
    m = j;
    c = 1ll * b * b % p;
    t = 1ll * t * c % p;
    r = 1ll * r * b % p;
  }
}
#line 5 "fps/relaxed.hpp"

template <class mint>
class RelaxedMultiply {
  const int B = 6;
  using fps = FormalPowerSeries<mint>;
  int n;
  fps f, g, h;
  vector<fps> f0, g0;

 public:
  RelaxedMultiply() : n(0), f(1), g(1), f0(B), g0(B) {}
  mint append(mint a, mint b) {
    f[n] = a, g[n] = b;
    n++;
    int m = n & -n;
    int l = __builtin_ctz((unsigned int)m);
    if (n == m) {
      f.resize(2 * m);
      g.resize(2 * m);
      h.resize(2 * m);
      if (l < B) {
        for (int i = 0; i < m; i++)
          for (int j = m - 1 - i; j < m; j++)
            h[i + j] += f[i] * g[j];
      } else {
        auto f1 = f;
        f1.ntt();
        f0.push_back(fps(f1.begin(), f1.begin() + m));
        auto g1 = g;
        g1.ntt();
        g0.push_back(fps(g1.begin(), g1.begin() + m));
        for (int i = 0; i < 2 * m; i++) f1[i] *= g1[i];
        f1.intt();
        for (int i = m - 1; i < 2 * m - 1; i++) h[i] += f1[i];
      }
    } else {
      if (l < B) {
        int s = n - m;
        for (int i = 0; i < m; i++) {
          int t = m - 1 - i;
          for (int j = 0; j < m; j++)
            h[n - 1 + j] += f[s + i] * g[t + j] + g[s + i] * f[t + j];
        }
      } else {
        fps f1(2 * m), g1(2 * m), h1(2 * m);
        copy(f.begin() + (n - m), f.begin() + n, f1.begin());
        copy(g.begin() + (n - m), g.begin() + n, g1.begin());
        f1.ntt(), g1.ntt();
        for (int i = 0; i < 2 * m; i++) h1[i] += f1[i] * g0[l + 1][i] + f0[l + 1][i] * g1[i];
        h1.intt();
        for (int i = m - 1; i < 2 * m - 1; i++) h[n - m + i] += h1[i];
      }
    }
    return h[n - 1];
  }
};

template <class mint>
class SemiRelaxedMultiply {
  const int B = 6;
  using fps = FormalPowerSeries<mint>;
  int n, m0;
  fps f, g, h;
  vector<fps> g0;

 public:
  SemiRelaxedMultiply(const fps& g_) : n(0), m0(1 << B), f(1), g(g_) {
    while (m0 < g.size()) m0 <<= 1;
    g.resize(m0);
    for (int k = 1; k <= m0; k <<= 1) {
      fps g1(2 * k);
      copy(g.begin(), g.begin() + min(2 * k, m0), g1.begin());
      g1.ntt();
      g0.push_back(g1);
    }
  }
  mint append(mint a) {
    f[n] = a;
    n++;
    int m = n & -n;
    int l = __builtin_ctz((unsigned int)m);
    if (n == m) {
      f.resize(2 * m);
      h.resize(2 * m);
    }
    while (l >= g0.size()) {
      g0.push_back(g0.back());
      g0.back().ntt_doubling();
    }
    if (l < B) {
      int s = n - m;
      for (int i = 0; i < m; i++) {
        int t = m - 1 - i;
        for (int j = 0; j < m; j++)
          h[n - 1 + j] += f[s + i] * g[t + j];
      }
    } else {
      fps f1(2 * m);
      copy(f.begin() + (n - m), f.begin() + n, f1.begin());
      f1.ntt();
      for (int i = 0; i < 2 * m; i++) f1[i] *= g0[l][i];
      f1.intt();
      for (int i = m - 1; i < 2 * m - 1; i++) h[n - m + i] += f1[i];
    }
    return h[n - 1];
  }
};

// f(x)/g(x)
template <class mint>
class RelaxedDivide {
  RelaxedMultiply<mint> mul;
  int n;
  mint c, v;

 public:
  RelaxedDivide() : n(0) {}
  mint append(mint a, mint b) { return v = n++ == 0 ? a * (c = b.inv()) : (a - mul.append(v, b)) * c; }
};

template <class mint>
class RelaxedInv {
  RelaxedMultiply<mint> mul;
  int n;
  mint c, v;

 public:
  RelaxedInv() : n(0) {}
  mint append(mint a) { return v = n++ == 0 ? (c = a.inv()) : -mul.append(v, a) * c; }
};

template <class mint>
class RelaxedExp {
  using fact = Factorial<mint>;
  RelaxedMultiply<mint> mul;
  int n;
  mint v;

 public:
  RelaxedExp() : n(0) {}
  mint append(mint a) {
    if (n++ == 0) {
      assert(a == 0);
      v = 1;
    } else {
      v = mul.append((n - 1) * a, v) * fact::inv(n - 1);
    }
    return v;
  }
};

template <class mint>
class RelaxedLog {
  using fact = Factorial<mint>;
  RelaxedMultiply<mint> mul;
  int n;
  mint a0, v;

 public:
  RelaxedLog() : n(0) {}
  mint append(mint a) {
    if (n == 0) {
      assert(a == 1);
      n++;
      return 0;
    } else if (n == 1) {
      a0 = a, n++;
      return v = a;
    } else {
      v = n * a - mul.append(v, a0);
      a0 = a;
      return v * fact::inv(n++);
    }
  }
};

template <class mint>
class RelaxedSqrt {
  RelaxedMultiply<mint> mul;
  int n;
  mint c, v;

 public:
  RelaxedSqrt() : n(0) {}
  mint append(mint a) {
    if (n == 0) {
      long long sq = ModSqrt(a.val(), mint::get_mod());
      assert(sq != -1 && sq != 0);
      c = mint(2 * sq).inv();
      n++;
      return sq;
    } else {
      return v = (n++ == 1 ? a : a - mul.append(v, v)) * c;
    }
  }
};

/**
 * @brief Relaxed 
 * @docs docs/fps/relaxed.md
 */

Back to top page